Building Complex Models¶
Checking for result changes¶
Tracking the effects of changes to complex models can get out of hand;
we recommend saving solutions with sol.save(), then checking that new solutions are almost equivalent
with sol1.almost_equal(sol2) and/or print(sol1.diff(sol2)), as shown below.
"Example code for solution saving and differencing."
import pickle
from gpkit import Model, Variable
# build model (dummy)
# decision variable
x = Variable("x")
y = Variable("y")
# objective and constraints
objective = 0.23 + x/y # minimize x and y
constraints = [x + y <= 5, x >= 1, y >= 2]
# create model
m = Model(objective, constraints)
# solve the model
# verbosity is 0 for testing's sake, no need to do that in your code!
sol = m.solve(verbosity=0)
# save the current state of the model
sol.save("last_verified.sol")
# uncomment the line below to verify a new model
last_verified_sol = pickle.load(open("last_verified.sol", mode="rb"))
if not sol.almost_equal(last_verified_sol, reltol=1e-3):
print(last_verified_sol.diff(sol))
# Note you can replace the last three lines above with
# print(sol.diff("last_verified.sol"))
# if you don't mind doing the diff in that direction.
You can also check differences between swept solutions, or between a point solution and a sweep.
Inheriting from Model¶
GPkit encourages an object-oriented modeling approach, where the modeler creates objects that inherit from Model to break large systems down into subsystems and analysis domains. The benefits of this approach include modularity, reusability, and the ability to more closely follow mental models of system hierarchy. For example: two different models for a simple beam, designed by different modelers, should be able to be used interchangeably inside another subsystem (such as an aircraft wing) without either modeler having to write specifically with that use in mind.
When you create a class that inherits from Model, write a .setup() method to create the model’s variables and return its constraints. GPkit.Model.__init__ will call that method and automatically add your model’s name and unique ID to any created variables.
Variables created in a setup method are added to the model even if they are not present in any constraints. This allows for simplistic ‘template’ models, which assume constant values for parameters and can grow incrementally in complexity as those variables are freed.
At the end of this page a detailed example shows this technique in practice.
Accessing Variables in Models¶
GPkit provides several ways to access a Variable in a Model (or ConstraintSet):
- using
Model.variables_byname(key). This returns all Variables in the Model, as well as in any submodels, that match the key. - using
Model.__getitem__.Model[key]returns the only variable matching the key, even if the match occurs in a submodel. If multiple variables match the key, an error is raised.
These methods are illustrated in the following example.
"Demo of accessing variables in models"
from gpkit import Model, Variable
class Battery(Model):
"""A simple battery
Upper Unbounded
---------------
m
Lower Unbounded
---------------
E
"""
def setup(self):
h = Variable("h", 200, "Wh/kg", "specific energy")
E = self.E = Variable("E", "MJ", "stored energy")
m = self.m = Variable("m", "lb", "battery mass")
return [E <= m*h]
class Motor(Model):
"""Electric motor
Upper Unbounded
---------------
m
Lower Unbounded
---------------
Pmax
"""
def setup(self):
m = self.m = Variable("m", "lb", "motor mass")
f = Variable("f", 20, "lb/hp", "mass per unit power")
Pmax = self.Pmax = Variable("P_{max}", "hp", "max output power")
return [m >= f*Pmax]
class PowerSystem(Model):
"""A battery powering a motor
Upper Unbounded
---------------
m
Lower Unbounded
---------------
E, Pmax
"""
def setup(self):
battery, motor = Battery(), Motor()
components = [battery, motor]
m = self.m = Variable("m", "lb", "mass")
self.E = battery.E
self.Pmax = motor.Pmax
return [components,
m >= sum(comp.m for comp in components)]
PS = PowerSystem()
print("Getting the only var 'E': %s" % PS["E"])
print("The top-level var 'm': %s" % PS.m)
print("All the variables 'm': %s" % PS.variables_byname("m"))
Getting the only var 'E': PowerSystem.Battery.E [MJ]
The top-level var 'm': PowerSystem.m [lb]
All the variables 'm': [gpkit.Variable(PowerSystem.Battery.m [lb]), gpkit.Variable(PowerSystem.Motor.m [lb]), gpkit.Variable(PowerSystem.m [lb])]
Vectorization¶
gpkit.Vectorize creates an environment in which Variables are created with an additional dimension:
"Example Vectorize usage, from gpkit/tests/t_vars.py"
from gpkit import Variable, Vectorize, VectorVariable
with Vectorize(3):
with Vectorize(5):
y = Variable("y")
x = VectorVariable(2, "x")
z = VectorVariable(7, "z")
assert(y.shape == (5, 3))
assert(x.shape == (2, 5, 3))
assert(z.shape == (7, 3))
This allows models written with scalar constraints to be created with vector constraints:
"Vectorization demonstration"
from gpkit import Model, Variable, Vectorize
class Test(Model):
"""A simple scalar model
Upper Unbounded
---------------
x
"""
def setup(self):
x = self.x = Variable("x")
return [x >= 1]
print("SCALAR")
m = Test()
m.cost = m["x"]
print(m.solve(verbosity=0).summary())
print("__________\n")
print("VECTORIZED")
with Vectorize(3):
m = Test()
m.cost = m["x"].prod()
m.append(m["x"][1] >= 2)
print(m.solve(verbosity=0).summary())
SCALAR
┃┓
Cost╺┫┃
(1) ┃┣╸1
┃┛
┃┓
Model╺┫┃
┃┣╸x ≥ 1
┃┛
Free Variables
--------------
x : 1
__________
VECTORIZED
┃┓
Cost╺┫┃
(2) ┃┣╸2
┃┛
┃┓ ┓
┃┃ ┃
┃┃ ┣╸x[0] ≥ 1
┃┃ ┛
┃┣╸Test1 ┓
Model╺┫┃ ┃
┃┃ ┣╸x[2] ≥ 1
┃┛ ┛
┃┓
┃┃
┃┣╸x[1] ≥ 2
┃┛
Free Variables
--------------
x : [ 1 2 1 ]
Multipoint analysis modeling¶
In many engineering models, there is a physical object that is operated in multiple conditions. Some variables correspond to the design of the object (size, weight, construction) while others are vectorized over the different conditions (speed, temperature, altitude). By combining named models and vectorization we can create intuitive representations of these systems while maintaining modularity and interoperability.
In the example below, the models Aircraft and Wing have a .dynamic() method which creates instances of AircraftPerformance and WingAero, respectively. The Aircraft and Wing models create variables, such as size and weight without fuel, that represent a physical object. The dynamic models create properties that change based on the flight conditions, such as drag and fuel weight.
This means that when an aircraft is being optimized for a mission, you can create the aircraft (AC in this example) and then pass it to a Mission model which can create vectorized aircraft performance models for each flight segment and/or flight condition.
The sensitivity diagram which this code outputs shows how it is organized (right-click and open in a new tab to see it more clearly):
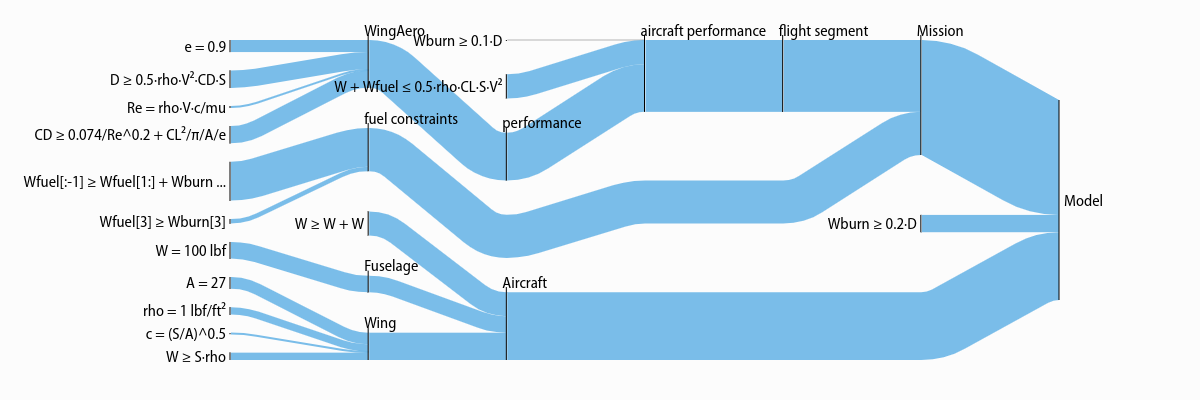
"""Modular aircraft concept"""
import pickle
import numpy as np
from gpkit import Model, Vectorize, parse_variables
class AircraftP(Model):
"""Aircraft flight physics: weight <= lift, fuel burn
Variables
---------
Wfuel [lbf] fuel weight
Wburn [lbf] segment fuel burn
Upper Unbounded
---------------
Wburn, aircraft.wing.c, aircraft.wing.A
Lower Unbounded
---------------
Wfuel, aircraft.W, state.mu
"""
@parse_variables(__doc__, globals())
def setup(self, aircraft, state):
self.aircraft = aircraft
self.state = state
self.wing_aero = aircraft.wing.dynamic(aircraft.wing, state)
self.perf_models = [self.wing_aero]
W = aircraft.W
S = aircraft.wing.S
V = state.V
rho = state.rho
D = self.wing_aero.D
CL = self.wing_aero.CL
return Wburn >= 0.1*D, W + Wfuel <= 0.5*rho*CL*S*V**2, {
"performance":
self.perf_models}
class Aircraft(Model):
"""The vehicle model
Variables
---------
W [lbf] weight
Upper Unbounded
---------------
W
Lower Unbounded
---------------
wing.c, wing.S
"""
@parse_variables(__doc__, globals())
def setup(self):
self.fuse = Fuselage()
self.wing = Wing()
self.components = [self.fuse, self.wing]
return [W >= sum(c.W for c in self.components),
self.components]
dynamic = AircraftP
class FlightState(Model):
"""Context for evaluating flight physics
Variables
---------
V 40 [knots] true airspeed
mu 1.628e-5 [N*s/m^2] dynamic viscosity
rho 0.74 [kg/m^3] air density
"""
@parse_variables(__doc__, globals())
def setup(self):
pass
class FlightSegment(Model):
"""Combines a context (flight state) and a component (the aircraft)
Upper Unbounded
---------------
Wburn, aircraft.wing.c, aircraft.wing.A
Lower Unbounded
---------------
Wfuel, aircraft.W
"""
def setup(self, aircraft):
self.aircraft = aircraft
self.flightstate = FlightState()
self.aircraftp = aircraft.dynamic(aircraft, self.flightstate)
self.Wburn = self.aircraftp.Wburn
self.Wfuel = self.aircraftp.Wfuel
return {"aircraft performance": self.aircraftp,
"flightstate": self.flightstate}
class Mission(Model):
"""A sequence of flight segments
Upper Unbounded
---------------
aircraft.wing.c, aircraft.wing.A
Lower Unbounded
---------------
aircraft.W
"""
def setup(self, aircraft):
self.aircraft = aircraft
with Vectorize(4): # four flight segments
self.fs = FlightSegment(aircraft)
Wburn = self.fs.aircraftp.Wburn
Wfuel = self.fs.aircraftp.Wfuel
self.takeoff_fuel = Wfuel[0]
return {
"fuel constraints":
[Wfuel[:-1] >= Wfuel[1:] + Wburn[:-1],
Wfuel[-1] >= Wburn[-1]],
"flight segment":
self.fs}
class WingAero(Model):
"""Wing aerodynamics
Variables
---------
CD [-] drag coefficient
CL [-] lift coefficient
e 0.9 [-] Oswald efficiency
Re [-] Reynold's number
D [lbf] drag force
Upper Unbounded
---------------
D, Re, wing.A, state.mu
Lower Unbounded
---------------
CL, wing.S, state.mu, state.rho, state.V
"""
@parse_variables(__doc__, globals())
def setup(self, wing, state):
self.wing = wing
self.state = state
c = wing.c
A = wing.A
S = wing.S
rho = state.rho
V = state.V
mu = state.mu
return [D >= 0.5*rho*V**2*CD*S,
Re == rho*V*c/mu,
CD >= 0.074/Re**0.2 + CL**2/np.pi/A/e]
class Wing(Model):
"""Aircraft wing model
Variables
---------
W [lbf] weight
S [ft^2] surface area
rho 1 [lbf/ft^2] areal density
A 27 [-] aspect ratio
c [ft] mean chord
Upper Unbounded
---------------
W
Lower Unbounded
---------------
c, S
"""
@parse_variables(__doc__, globals())
def setup(self):
return [c == (S/A)**0.5,
W >= S*rho]
dynamic = WingAero
class Fuselage(Model):
"""The thing that carries the fuel, engine, and payload
A full model is left as an exercise for the reader.
Variables
---------
W 100 [lbf] weight
"""
@parse_variables(__doc__, globals())
def setup(self):
pass
AC = Aircraft()
MISSION = Mission(AC)
M = Model(MISSION.takeoff_fuel, [MISSION, AC])
print(M)
sol = M.solve(verbosity=0)
# save solution to some files
sol.savemat()
sol.savecsv()
sol.savetxt()
sol.save("solution.pkl")
# retrieve solution from a file
sol_loaded = pickle.load(open("solution.pkl", "rb"))
vars_of_interest = set(AC.varkeys)
# note that there's two ways to access submodels
assert (MISSION["flight segment"]["aircraft performance"]
is MISSION.fs.aircraftp)
vars_of_interest.update(MISSION.fs.aircraftp.unique_varkeys)
vars_of_interest.add(M["D"])
print(sol.summary(vars_of_interest))
print(sol.table(tables=["loose constraints"]))
M.append(MISSION.fs.aircraftp.Wburn >= 0.2*MISSION.fs.aircraftp.wing_aero.D)
sol = M.solve(verbosity=0)
print(sol.diff("solution.pkl", showvars=vars_of_interest, sortbymodel=False))
try:
from gpkit.interactive.sankey import Sankey
variablesankey = Sankey(sol, M).diagram(AC.wing.A)
sankey = Sankey(sol, M).diagram(width=1200, height=400, maxlinks=30)
# the line below shows an interactive graph if run in jupyter notebook
sankey # pylint: disable=pointless-statement
except (ImportError, ModuleNotFoundError):
print("Making Sankey diagrams requires the ipysankeywidget package")
from gpkit.interactive.references import referencesplot
referencesplot(M, openimmediately=False)
Note that the output table has been filtered above to show only variables of interest.
Cost Function
-------------
Wfuel[0]
Constraints
-----------
Mission
"fuel constraints":
Wfuel[:-1] ≥ Wfuel[1:] + Wburn[:-1]
Wfuel[3] ≥ Wburn[3]
FlightSegment
AircraftP
Wburn[:] ≥ 0.1·D[:]
Aircraft.W + Wfuel[:] ≤ 0.5·Mission.FlightSegment.FlightState.rho[:]·CL[:]·S·V[:]²
"performance":
WingAero
D[:] ≥ 0.5·Mission.FlightSegment.FlightState.rho[:]·V[:]²·CD[:]·S
Re[:] = Mission.FlightSegment.FlightState.rho[:]·V[:]·c/mu[:]
CD[:] ≥ 0.074/Re[:]^0.2 + CL[:]²/π/A/e[:]
FlightState
(no constraints)
Aircraft
Aircraft.W ≥ Fuselage.W + Wing.W
Fuselage
(no constraints)
Wing
c = (S/A)^0.5
Wing.W ≥ S·Wing.rho
┃┓ ┓ ┓ ┓ ┓
┃┃ ┃ ┃ ┃ ┃
┃┃ ┃ ┃ ┣╸Wburn[2] ┣╸CD[2]╶⎨
┃┃ ┃ ┃ ┃ (0.272lbf) ┃ (0.0189)
┃┃ ┃ ┃ ┛ ┛
┃┃ ┃ ┣╸Wfuel[2] ┓ ┓
┃┃ ┃ ┃ (0.544lbf) ┃ ┃
┃┃ ┣╸Wfuel[1] ┃ ┣╸Wfuel[3] ┣╸CD[3]╶⎨
┃┃ ┃ (0.817lbf) ┃ ┃ (0.272lbf) ┃ (0.0188)
Cost╺┫┃ ┃ ┛ ┛ ┛
(1.09lbf) ┃┣╸Wfuel[0] ┃ ┓ ┓ ┓
┃┃ (1.09lbf) ┃ ┃ ┃ ┣╸CL[1]²
┃┃ ┃ ┣╸Wburn[1] ┣╸CD[1] ┛ (1.01)
┃┃ ┃ ┃ (0.273lbf) ┃ (0.0189) ┣╸1/Re[1]^0.2
┃┃ ┛ ┛ ┛ ┛ (0.0772)
┃┃ ┓ ┓ ┓
┃┃ ┃ ┃ ┣╸CL[0]²
┃┃ ┣╸Wburn[0] ┣╸CD[0] ┛ (1.01)
┃┃ ┃ (0.274lbf) ┃ (0.019) ┣╸1/Re[0]^0.2
┃┛ ┛ ┛ ┛ (0.0772)
┃┓ ┓ ┓
┃┃ ┃ ┃
┃┃ ┃ ┃
┃┃ ┃ ┃
┃┃ ┣╸FlightSegment ┣╸AircraftP╶⎨
┃┃ ┃ ┃
┃┣╸Mission ┃ ┃
┃┃ ┃ ┃
┃┃ ┛ ┛
Model╺┫┃ ┣╸Wfuel[0] ≥ Wfuel[1] + Wburn[0]
┃┃ ┛
┃┃ ┣╸Wfuel[1] ≥ Wfuel[2] + Wburn[1]
┃┛ ┣╸Wfuel[2] ≥ Wfuel[3] + Wburn[2]
┃┓ ┓
┃┃ ┣╸Wing╶⎨
┃┃ ┛
┃┣╸Aircraft ┣╸W ≥ Fuselage.W + Wing.W
┃┃ ┛
┃┃ ┣╸Fuselage ┣╸W = 100lbf
┃┛ ┛ ┛
Free Variables
--------------
| Aircraft
W : 144.1 [lbf] weight
| Aircraft.Wing
S : 44.14 [ft²] surface area
W : 44.14 [lbf] weight
c : 1.279 [ft] mean chord
| Mission.FlightSegment.AircraftP
Wburn : [ 0.274 0.273 0.272 0.272 ] [lbf] segment fuel burn
Wfuel : [ 1.09 0.817 0.544 0.272 ] [lbf] fuel weight
| Mission.FlightSegment.AircraftP.WingAero
D : [ 2.74 2.73 2.72 2.72 ] [lbf] drag force
Insensitive Constraints |below +1e-05|
--------------------------------------
(none)
Solution Diff (for selected variables)
======================================
(argument is the baseline solution)
Constraint Differences
**********************
@@ -31,3 +31,4 @@
Wing
c = (S/A)^0.5
Wing.W ≥ S·Wing.rho
+ Wburn[:] ≥ 0.2·D[:]
**********************
Relative Differences |above 1%|
-------------------------------
Wburn : [ +102.1% +101.6% +101.1% +100.5% ] segment fuel burn
Wfuel : [ +101.3% +101.1% +100.8% +100.5% ] fuel weight
D : [ +1.1% - - - ] drag force